아직도 자신이 없는 DP를 자신 있을 때까지 파보기로 하자.
DP는 작은 문제의 결과를 저장해놓고, 이를 이용해 큰 문제를 푸는 방식이다.
거스름돈을 2원과 5원을 사용해서 최소 개수만큼 돌려주고 싶다.
처음엔 그리디 알고리즘으로 접근하였다. 5원으로 먼저 거슬러 주고 남은 금액을 2원으로 주는 것이다.
😶🌫️ 코드 보기🔽
처음 생각한 코드 - DP로 접근하지 않았따!
#include <iostream>
using namespace std;
int main()
{
int n, count = 0;
cin >> n;
count += n / 5;
n = n % 5 ;
while(count >= 0)
{
if(n % 2 == 0)
{
count += n / 2;
break;
}
count--;
n += 5;
}
cout << (count > 0 ? count : -1);
return 0;
}
DP는 어떻게 접근하면 좋을까?
큰 문제를 작게 생각은 어떻게 하는 걸까?..
일단 거슬러야 하는 금액이 0원부터 생각해 본다.
0원이면 거스름돈은 0원이다.
1원이라면 거슬러 줄 수 없어서 -1을 출력한다.
2원은 2원 하나를 주면 되고,
3원은 거슬러 줄 수 없기에 -1,
4원은 2원 두 개,
5원은 5원 한 개,
6원은 2원 3개,
7원은 5원 1개 2원 한 개,
8원은 2원 4개,
10원은 2원 5개, 5원 2개,
.
.
.
어떤 금액 n을 거슬러 줘야 한다고 할 때
n에서 2원을 하나 사용해서 거슬러 주는 방법과
n에서 5원을 하나 사용해서 거슬러 주는 방법이 있을 것이다.
작은 문제 정의:
어떤 금액 n에서 2원 또는 5원을 사용했을 때, 남은 금액의 최소 동전 개수를 계산하여
현재 금액의 최소 동전 개수를 구할 수 있습니다.
어떤 금액 n에 대해
dp[n] = min(dp[n − 2] + 1, dp[n − 5] + 1)
n에서 2원을 하나 사용한 경우 (n - 2)와
5원을 하나를 사용한 경우 (n - 5) 중 최솟값을 선택하자
100이라면? 1000이라면? 이런 큰 문제를 작게 -> 1원이라면 6원이라면? 으로 작은 문제로 먼저 보는 것이다.
왜? 그것이 DP이기 때문..
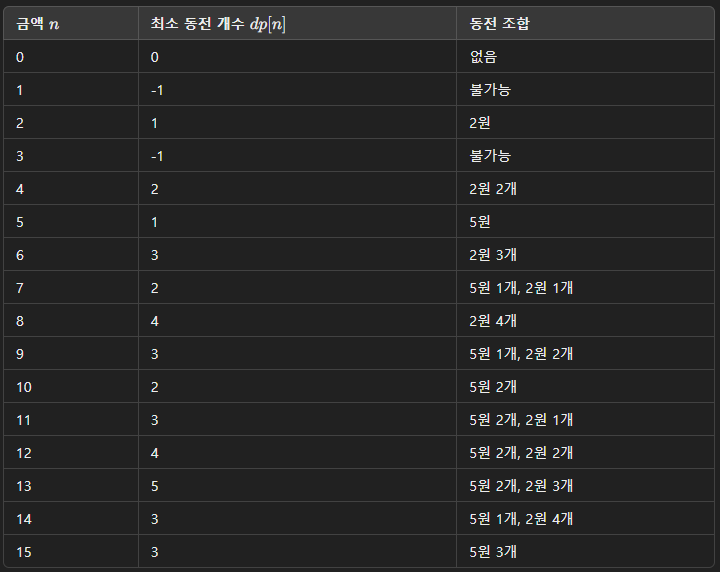
금액 n을 0부터 계산해 본다면 다음과 같을 것이다.
😶🌫️ 코드 보기🔽
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int maxValue = 1e9;
int main()
{
int n;
cin >> n;
vector<int> dp(n + 1, maxValue);
dp[0] = 0;
for(int idx = 1; idx <= n; ++idx)
{
if(idx >= 2)
{
dp[idx] = min(dp[idx], dp[idx - 2] + 1);
}
if(idx >= 5)
{
dp[idx] = min(dp[idx], dp[idx - 5] + 1);
}
}
cout << (dp[n] == maxValue ? -1 : dp[n]);
return 0;
}
DP는 익숙하지 않아서 피해왔는데 지금부터는 깨부수기 위해 노력할 것이다.


😶🌫️ 깨알 상식 보기🔽
작은 문제에서 시작해 점진적으로 큰 문제를 해결하는 방식을 Bottom-up 방식이라고 한다.
for문을 주로 사용하여 점진적 계산을 한다.
반대로 큰 문제에서 시작하여 작은 문제를 해결하는 방식을 Top-down 방식이라고 한다.
재귀 함수 형태로 구현하여 큰 문제를 작게 쪼개고, 작은 문제를 해결하여 결과를 저장한다.
'Algorithms' 카테고리의 다른 글
| Hackerrank_Lily's Homework_사이클 분할 (0) | 2024.10.27 |
|---|---|
| HackerRank_Medium_Common Child && 스택의 비밀 (2) | 2024.07.18 |
| Programmers_Level3_징검다리 건너기 (2) | 2024.07.04 |
| Programmers_Level3_기지국 설치 (2) | 2024.06.07 |
| Programmers_Level2_게임 맵 최단거리 (2) | 2024.06.06 |
아직도 자신이 없는 DP를 자신 있을 때까지 파보기로 하자.

DP는 작은 문제의 결과를 저장해놓고, 이를 이용해 큰 문제를 푸는 방식이다.
거스름돈을 2원과 5원을 사용해서 최소 개수만큼 돌려주고 싶다.
처음엔 그리디 알고리즘으로 접근하였다. 5원으로 먼저 거슬러 주고 남은 금액을 2원으로 주는 것이다.
😶🌫️ 코드 보기🔽
처음 생각한 코드 - DP로 접근하지 않았따!
#include <iostream> using namespace std; int main() { int n, count = 0; cin >> n; count += n / 5; n = n % 5 ; while(count >= 0) { if(n % 2 == 0) { count += n / 2; break; } count--; n += 5; } cout << (count > 0 ? count : -1); return 0; }
DP는 어떻게 접근하면 좋을까?
큰 문제를 작게 생각은 어떻게 하는 걸까?..
일단 거슬러야 하는 금액이 0원부터 생각해 본다.
0원이면 거스름돈은 0원이다.
1원이라면 거슬러 줄 수 없어서 -1을 출력한다.
2원은 2원 하나를 주면 되고,
3원은 거슬러 줄 수 없기에 -1,
4원은 2원 두 개,
5원은 5원 한 개,
6원은 2원 3개,
7원은 5원 1개 2원 한 개,
8원은 2원 4개,
10원은 2원 5개, 5원 2개,
.
.
.
어떤 금액 n을 거슬러 줘야 한다고 할 때
n에서 2원을 하나 사용해서 거슬러 주는 방법과
n에서 5원을 하나 사용해서 거슬러 주는 방법이 있을 것이다.
작은 문제 정의:
어떤 금액 n에서 2원 또는 5원을 사용했을 때, 남은 금액의 최소 동전 개수를 계산하여
현재 금액의 최소 동전 개수를 구할 수 있습니다.
어떤 금액 n에 대해 dp[n] = min(dp[n − 2] + 1, dp[n − 5] + 1) n에서 2원을 하나 사용한 경우 (n - 2)와 5원을 하나를 사용한 경우 (n - 5) 중 최솟값을 선택하자
100이라면? 1000이라면? 이런 큰 문제를 작게 -> 1원이라면 6원이라면? 으로 작은 문제로 먼저 보는 것이다.
왜? 그것이 DP이기 때문..
금액 n을 0부터 계산해 본다면 다음과 같을 것이다.

😶🌫️ 코드 보기🔽
#include <iostream> #include <vector> #include <algorithm> using namespace std; const int maxValue = 1e9; int main() { int n; cin >> n; vector<int> dp(n + 1, maxValue); dp[0] = 0; for(int idx = 1; idx <= n; ++idx) { if(idx >= 2) { dp[idx] = min(dp[idx], dp[idx - 2] + 1); } if(idx >= 5) { dp[idx] = min(dp[idx], dp[idx - 5] + 1); } } cout << (dp[n] == maxValue ? -1 : dp[n]); return 0; }
DP는 익숙하지 않아서 피해왔는데 지금부터는 깨부수기 위해 노력할 것이다.


😶🌫️ 깨알 상식 보기🔽
작은 문제에서 시작해 점진적으로 큰 문제를 해결하는 방식을 Bottom-up 방식이라고 한다.
for문을 주로 사용하여 점진적 계산을 한다.
반대로 큰 문제에서 시작하여 작은 문제를 해결하는 방식을 Top-down 방식이라고 한다.
재귀 함수 형태로 구현하여 큰 문제를 작게 쪼개고, 작은 문제를 해결하여 결과를 저장한다.
'Algorithms' 카테고리의 다른 글
| Hackerrank_Lily's Homework_사이클 분할 (0) | 2024.10.27 |
|---|---|
| HackerRank_Medium_Common Child && 스택의 비밀 (2) | 2024.07.18 |
| Programmers_Level3_징검다리 건너기 (2) | 2024.07.04 |
| Programmers_Level3_기지국 설치 (2) | 2024.06.07 |
| Programmers_Level2_게임 맵 최단거리 (2) | 2024.06.06 |
